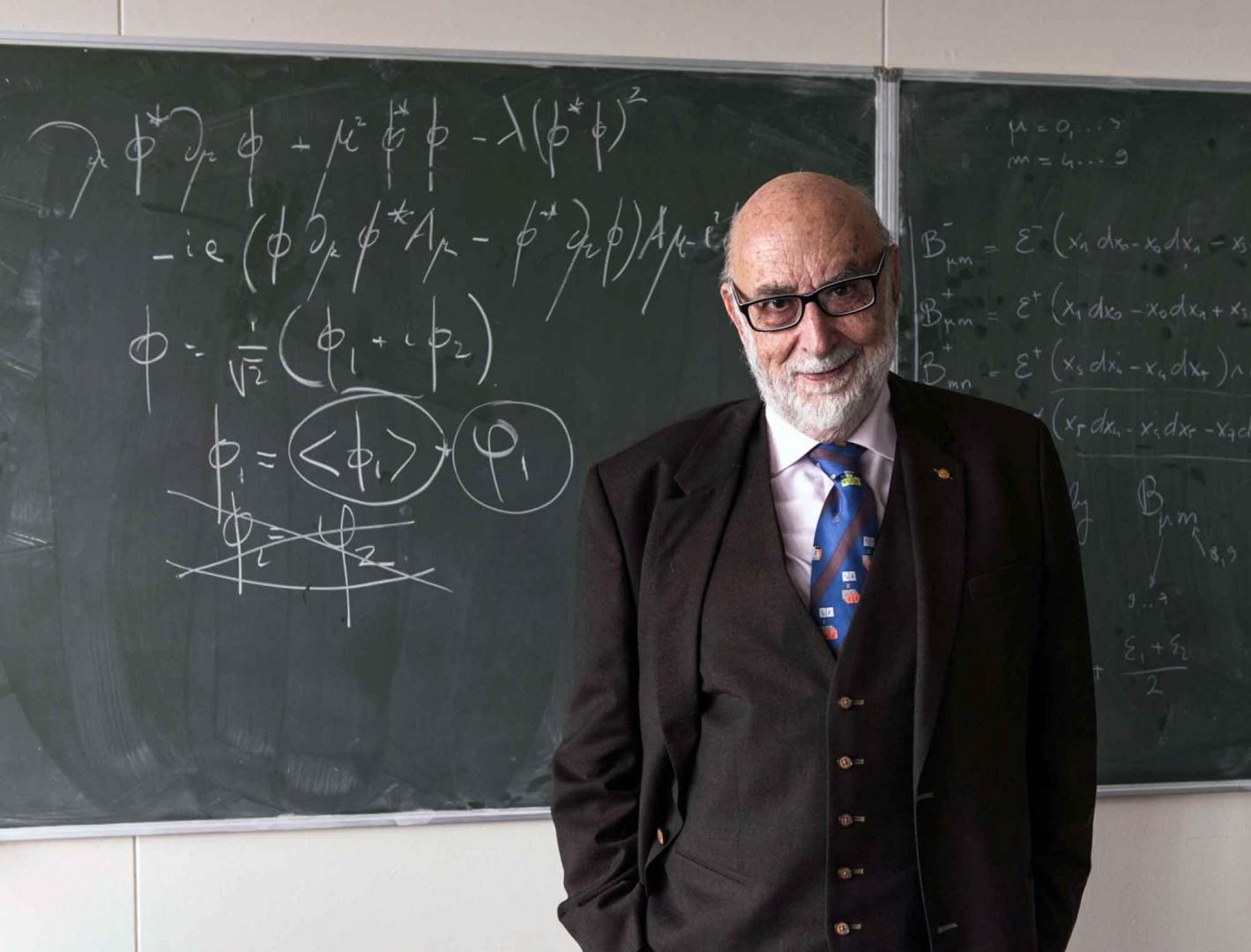A Nobel laureate and a blackboard at CERN is all you need to explain the fundamental physics of the universe. At least, that's what François Englert convinced us on his visit to CERN last week.
Englert shared the 2013 Nobel prize in physics with Peter Higgs "for the theoretical discovery of a mechanism that contributes to our understanding of the origin of mass of subatomic particles". In the video below, he explains how he and Higgs manipulated equations containing mathematical constructs called scalar fields to predict the existence of the Brout-Englert-Higgs field.
According to Englert, the equation describing this mechanism is built in two parts. One part consists of scalar fields; the other consists of constructs called gauge fields. Englert explains that a big problem in particle physics in the 1960s was to find a gauge field that had mass. Solving that problem - working out how a gauge field could have mass -would help to explain other problems in physics, such as how to mathematically describe short-range interactions inside the nuclei of atoms. But Englert says that you cannot easily just add mass to a gauge field "off-hand". He needed another theoretical approach.
The key was to add a new part – a new scalar field – to the equation describing the mass mechanism. Part of this new scalar field could be mathematically simplified. What came out of the algebraic manipulation was a term that gave rise to "a condensate spread out all over the universe". Then, the interaction between the condensate and another part of the equation could be generalized, says Englert, to give mass to elementary particles. Easy peasy!
"I know this is extremely abstract," says a modest Englert of his explanation. "But if I have two minutes [to explain it], I can hardly do more!"
Find out more about the Higgs boson in the pages below.