
When a new particle physics discovery is made, you may have heard the term “sigma” being used. What does this mean? Why is it so important to talk about sigma when making a claim for a new particle discovery? And why is five sigma in particular so important?
Why does particle physics rely on statistics?
Particles produced in collisions in the Large Hadron Collider (LHC) are tiny and extremely short-lived. Because they almost immediately decay into further particles, it is impossible for physicists to directly “see” them. Instead, they look at the properties of the final particles, such as their charge, mass, spin and velocity. They work like detectives: the end products provide clues to the possible transformations that the particles underwent as they decayed. The probabilities of these so-called “decay channels” are predicted by theory.
In the LHC, millions of particle collisions per second are tracked by the detectors and filtered through trigger systems to identify decays of rare particles. Scientists then analyse the filtered data to look for anomalies, which can indicate new physics.
As with any experiment, there is always a chance of error. Background noise can cause natural fluctuations in the data resulting in statistical error. There is also potential for error if there isn’t enough data, or systematic error caused by faulty equipment or small mistakes in calculations. Scientists look for ways to reduce the impact of these errors to ensure that the claims they make are as accurate as possible.
What is statistical significance?
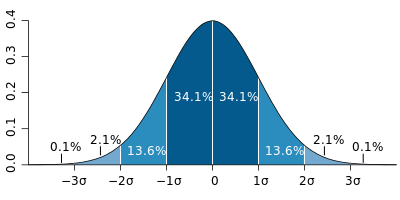
Imagine rolling a standard die. There is a one in six probability of getting one number. Now imagine rolling two dice – the probability of getting a certain total number varies – there is only one way to roll a two, and six different ways to roll a seven. If you were to roll two dice many, many times and record your results, the shape of the graph would follow a bell-curve known as a normal distribution.
The normal distribution has some interesting properties. It is symmetrical, its peak is called the mean and the data spread is measured using standard deviation. For data that follows a normal distribution, the probability of a data point being within one standard deviation of the mean value is 68%, within two is 95%, within three is even higher.
Standard deviation is represented by the Greek letter σ, or sigma. Measured by numbers of standard deviations from the mean, statistical significance is how far away a certain data point lies from its expected value.
What has this got to do with physics?
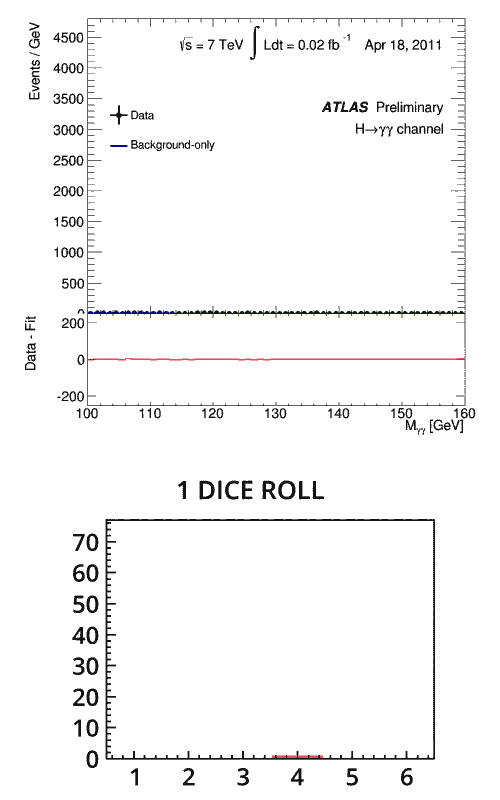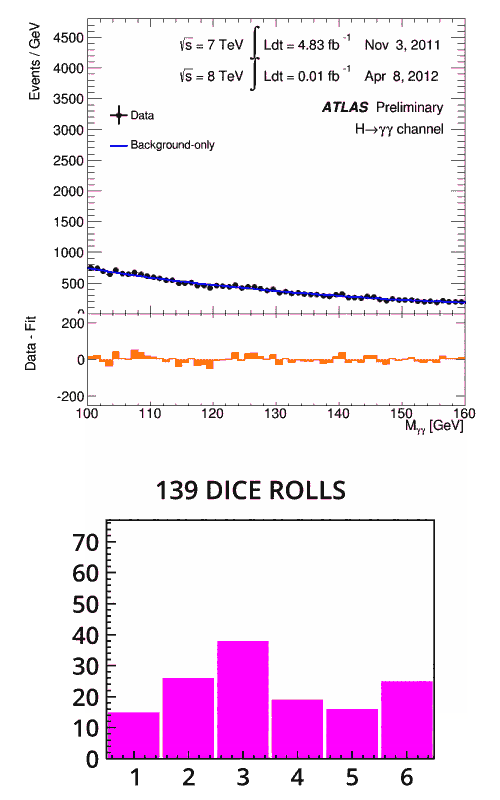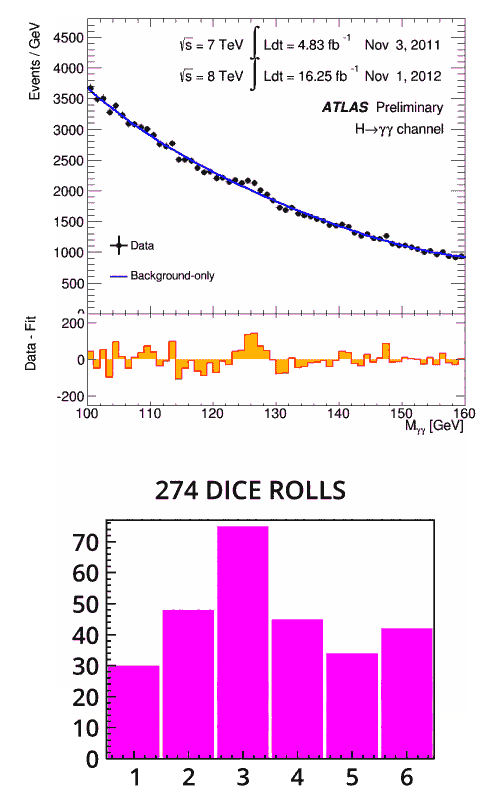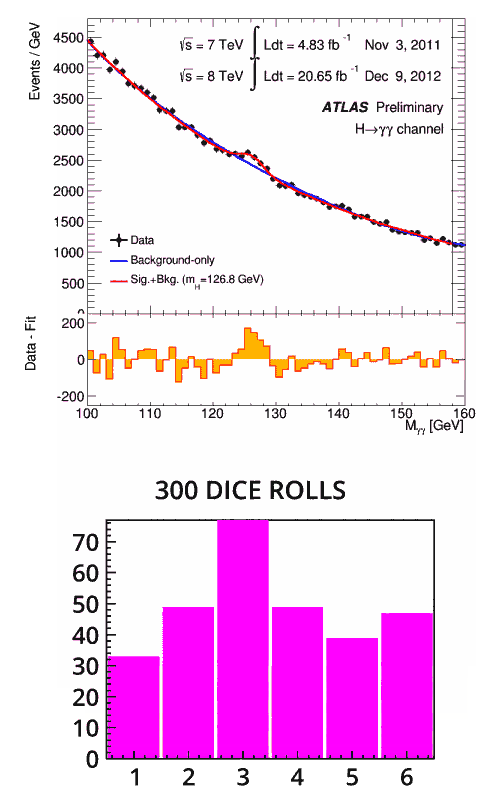
Second image: Animation of the results of 300 dice rolls, where the die has been manipulated to show the number 3 more often than expected. (Image: Piotr Traczyk/CERN)
When scientists record data from the LHC, it is natural that there are small bumps and statistical fluctuations, but these are generally close to the expected value. There is an indication of a new result when there is a larger anomaly. At which point can this anomaly be classified as a new phenomenon? Scientists use statistics to find this out.
Imagine the dice metaphor again. Except this time, you are rolling one die, but you do not know if it is weighted. You roll it once and get a three. There is nothing particularly significant about this – there was a one in six chance of your result – you need more data to determine if it is weighted. You roll it twice, three times, or even more, and every time it lands on a three. At what point can you confirm it is weighted?
There isn’t a particular rule for this, but after around eight times of getting the same number, you’d be pretty certain that it was. The chance of this happening as a fluke is only (1/6)8 = 0.00006%.
In the same way, this is how physicists determine if an anomaly is indeed a result. With more and more data, the likelihood of a statistical fluctuation at a specific point gets smaller and smaller. In the case of the Higgs boson, physicists needed enough data for the statistical significance to pass the threshold of five sigma. Only then could they announce the discovery of “a Higgs-like particle.”
What does it mean when physicists say data has a statistical significance of five sigma?
A result that has a statistical significance of five sigma means the almost certain likelihood that a bump in the data is caused by a new phenomenon, rather than a statistical fluctuation. Scientists calculate this by measuring the signal against the expected fluctuations in the background noise across the whole range. For some results, whose anomalies could lie in either direction above or below the expected value, a significance of five sigma is the 0.00006% chance the data is fluctuation. For other results, like the Higgs boson discovery, a five-sigma significance is the 0.00003% likelihood of a statistical fluctuation, as scientists look for data that exceeds the five-sigma value on one half of the normal distribution graph.
Why is five sigma specifically important for particle physics?
In most areas of science that use statistical analysis, the five-sigma threshold seems overkill. In a population study, such as polls for how people will vote, usually a result with three sigma statistical significance would suffice. However, when discussing the very fabric of the Universe, scientists aim to be as precise as possible. The results of the fundamental nature of matter are high impact and have significant repercussions if they are wrong.
In the past, physicists have noticed results that could indicate new discoveries, with the data having only three to four sigma statistical significance. These have often been disproven as more data is collected.
If there is a systematic error, such as a miscalculation, the high initial significance of five sigma may mean that the results are not completely void. However, this means that the result is not definite and cannot be used to make a claim for a new discovery.
Five sigma is considered the “gold standard” in particle physics because it guarantees an extremely low likelihood of a claim being false.
But not all five sigmas are equal…
Five sigma is generally the accepted value for statistical significance for finding new particles within the Standard Model – those particles that are predicted by theory and lie within our current understanding of nature. Five sigma significance is also accepted when searching for specific properties of particle behaviour, as there is less chance of finding fluctuations elsewhere in the range.
Whether five sigma is enough statistical significance can be determined by comparing the probability of the new hypothesis with the chance it is a statistical fluctuation, taking the theory into account.
For physics beyond the Standard Model, or data that contradicts generally accepted physics, a much higher value of statistical significance is required – effectively enough to “disprove” the previous physics. In his paper “The significance of five sigma,” physicist Louis Lyons suggests that results for more unlikely phenomena should have a higher statistical significance, such as seven sigma for the detection of gravitational waves or the discovery of pentaquarks.
In this paper, Lyons also deems five sigma statistical significance to be enough for the Higgs boson discovery. This is because the theory for the Higgs boson had been predicted, mathematically tested, and generally accepted by the particle physics community well-before the LHC could generate conditions to be able to observe it. But once this was achieved, it still required a high statistical significance to determine if the signal detected was indeed a discovery.
___________________________________________________________________________
A statistical significance of five sigma is rigorous, but it is really a minimum. A higher value for statistical significance cements data as being more reliable. However, achieving results with statistical significance of six, seven, or even eight sigma requires a lot more data, a lot more time, and a lot more energy. In other words, a probability of at most 0.00006% that a new phenomenon is not a statistical fluke is good enough.
Find out more:
- Paper: The significance of five sigma
- Video: The Higgs boson discovery, explained
- Online article: One and two sided probability

